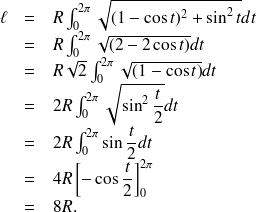Intégrale curviligne

En géométrie différentielle, l'intégrale curviligne est une intégrale où la fonction à intégrer est évaluée sur une courbe Γ. Il y a deux types d'intégrales curvilignes, selon que la fonction est à valeurs réelles ou à valeurs dans les formes linéaires. Le second type (qui peut se reformuler en termes de circulation d'un champ de vecteurs) a comme cas particulier les intégrales que l'on considère en analyse complexe.

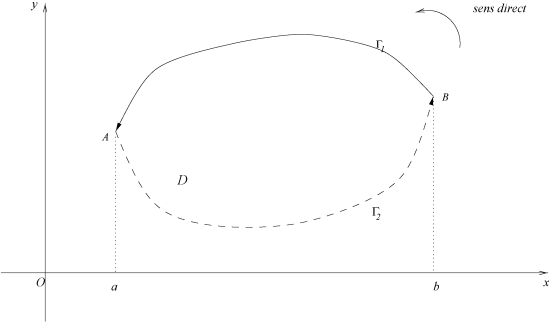
Dans cet article, Γ est un arc orienté dans ℝⁿ, rectifiable c'est-à-dire paramétré par une fonction continue à variation bornée t ↦ γ(t), avec t ∈ [a, b].

Intégrale d'un champ scalaire

On définit l'intégrale curviligne d'un champ scalaire continu ${\displaystyle f:\Gamma \to \mathbb {R} }$ comme l'intégrale de Stieltjes de f∘γ par rapport à l'abscisse curviligne s_γ(t) (longueur de l'arc γ restreint à [a, t]) :

${\displaystyle \int _{\Gamma }f\ \mathrm {d} s=\int _{a}^{b}(f\circ \gamma )\,\mathrm {d} s_{\gamma },}$

c'est-à-dire la limite, quand le pas de la subdivision pointée de [a, b] tend vers 0, des sommes de Riemann associées :${\displaystyle \sum _{k=1}^{n}f(\gamma (t'_{k}))\left(s_{\gamma }(t_{k})-s_{\gamma }(t_{k-1})\right)}$ où la subdivision pointée est notée : a = t₀ < t₁ < … < t_n = b, t'_k ∈ [t_k–1, t_k].

Cette définition ne dépend pas du paramétrage de Γ, ni de l'orientation.

La longueur s_γ(b) de l'arc Γ est l'intégrale curviligne de la fonction constante 1.

Si γ est de classe C¹, ${\displaystyle \int _{\Gamma }f\ \mathrm {d} s=\int _{a}^{b}f(\gamma (t))\|\gamma '(t)\|\mathrm {d} t.}$

Analyse vectorielle

On définit également la circulation le long de Γ d'un champ vectoriel continu ${\displaystyle f:\Gamma \to \mathbb {R} ^{n}}$ comme une intégrale de Stieltjes :

${\displaystyle \int _{\Gamma }f\cdot \,\mathrm {d} \gamma =\int _{a}^{b}(f\circ \gamma )\cdot \,\mathrm {d} \gamma ,}$

où ∙ désigne le produit scalaire.

Cette définition ne dépend pas du paramétrage de Γ mais dépend de l'orientation (l'intégrale est changée en son opposée quand la courbe est parcourue en sens inverse).

On peut reformuler cette définition en notant ω la 1-forme différentielle « produit scalaire par f » : si ω est une 1-forme différentielle continue sur le support de Γ, on définit l'intégrale curviligne de ω le long de Γ par :

${\displaystyle \int _{\Gamma }\omega =\int _{a}^{b}\langle \omega \circ \gamma ,\mathrm {d} \gamma \rangle ,}$

où ⟨∙, ∙⟩ est le crochet de dualité.

Si γ est de classe C¹,${\displaystyle \int _{\Gamma }f\cdot \,\mathrm {d} \gamma =\int _{a}^{b}f(\gamma (t))\cdot \gamma '(t)\,\mathrm {d} t\quad {\rm {et}}\quad \int _{\Gamma }\omega =\int _{a}^{b}\omega _{\gamma (t)}(\gamma '(t))\,\mathrm {d} t.}$

Analyse complexe

Pour n = 2 et en identifiant ℝ² au plan complexe, on définit l'intégrale curviligne d'une fonction continue ${\displaystyle f:\Gamma \to \mathbb {C} }$ comme l'intégrale de la 1-forme différentielle « produit (complexe) par f » :

${\displaystyle \int _{\Gamma }f(z)\,\mathrm {d} z=\int _{a}^{b}(f\circ \gamma )\,\mathrm {d} \gamma .}$

Si γ est de classe C¹, ${\displaystyle \int _{\Gamma }f(z)\,\mathrm {d} z=\int _{a}^{b}f(\gamma (t))\gamma '(t)\,\mathrm {d} t.}$

Lorsque Γ est une courbe fermée (ses deux extrémités coïncident), il arrive qu'on utilise la notation : ${\displaystyle \oint _{\Gamma }f(z)\,\mathrm {d} z.}$

Exemple

Soit la fonction f(z) = 1/z, et soit C le cercle unité parcouru une fois dans le sens trigonométrique, ce qui peut se paramétrer par e^it, avec t parcourant [0, 2π]. L'intégrale correspondante est ${\displaystyle \oint _{C}f(z)\,\mathrm {d} z=\int _{0}^{2\pi }{1 \over {\rm {e}}^{{\rm {i}}t}}{\rm {i}}{\rm {e}}^{{\rm {i}}t}\,\mathrm {d} t=\int _{0}^{2\pi }{\rm {i}}\,\mathrm {d} t=2i\pi .}$

Propriétés

Les propriétés fondamentales des intégrales curvilignes sont le théorème intégral de Cauchy et la formule intégrale de Cauchy, qui permettent d'établir le théorème des résidus.

Références

Articles connexes

• Théorème de Stokes
• Intégrale de surface
• Méthodes de calcul d'intégrales de contour

• Portail de l'analyse