Théorème de Lie

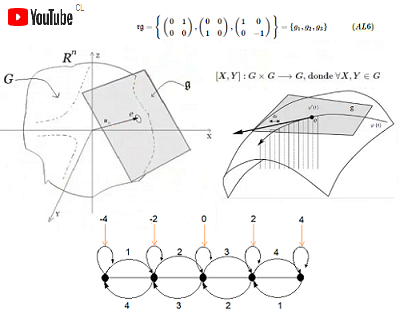
En mathématiques, le théorème de Lie, démontré en 1876 par Sophus Lie, porte sur la structure des algèbres de Lie résolubles. Comme les théorèmes de Engel (1890) et de Kolchin (1948), il s'agit d'un théorème de trigonalisation simultanée.

Le théorème s'énonce ainsi :

Une conséquence très importante de ce théorème est le critère de Cartan. On suppose ici simplement K de caractéristique nulle. Pour ${\displaystyle {\mathfrak {g}}}$ comme ci-dessus, on note B la forme bilinéaire sur ${\displaystyle {\mathfrak {g}}}$ définie par B(X, Y) = tr(XY). B est la forme de Killing associée à ${\displaystyle {\mathfrak {g}}}$. Le critère de Cartan montre alors que ${\displaystyle {\mathfrak {g}}}$ est résoluble si et seulement si ${\displaystyle B({\mathfrak {g}},D{\mathfrak {g}})=0}$, où ${\displaystyle D{\mathfrak {g}}=[{\mathfrak {g}},{\mathfrak {g}}]}$.

Ce théorème est à son tour très utile pour établir le critère de Killing-Cartan : avec la même hypothèse sur K, ${\displaystyle {\mathfrak {g}}}$ est semi-simple si et seulement si B est une forme bilinéaire non dégénérée. Ce critère est le premier pas vers la classification des algèbres de Lie semi-simples.

Notes et référence

Liens externes

• Portail de l’algèbre