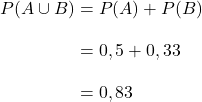Événements incompatibles

Deux événements ${\displaystyle E}$ et ${\displaystyle F}$ d'une expérience aléatoire sont dits incompatibles (ou disjoints) lorsqu'ils n'ont aucune éventualité en commun, c'est-à-dire lorsque l'intersection des sous-ensembles ${\displaystyle E}$ et ${\displaystyle F}$ est vide : ${\displaystyle E\cap F=\emptyset }$.

Autrement dit, ces deux événements sont incompatibles si et seulement si la réalisation simultanée de ${\displaystyle E}$ et ${\displaystyle F}$ est impossible.

Si ${\displaystyle E}$ et ${\displaystyle F}$ sont deux événements incompatibles, on a alors : ${\displaystyle \mathbb {P} (E\cup F)=\mathbb {P} (E) \mathbb {P} (F)}$.
Si ${\displaystyle E}$ et ${\displaystyle F}$ sont deux événements compatibles, on a alors : ${\displaystyle \mathbb {P} (E\cup F)=\mathbb {P} (E) \mathbb {P} (F)-\mathbb {P} (E\cap F)}$.

Attention à ne pas confondre cette notion avec celle d'événements indépendants. En fait, deux événements ${\displaystyle E}$ et ${\displaystyle F}$ de probabilités non nulles ne peuvent être à la fois incompatibles et indépendants.

À noter qu'il faut distinguer les événements incompatibles des événements contraires, qui se démarquent par le fait que ${\displaystyle \mathbb {P} (A) \mathbb {P} (B)=1}$.

Voir aussi

• Axiomes des probabilités

• Portail des probabilités et de la statistique