Variations séculaires des orbites planétaires

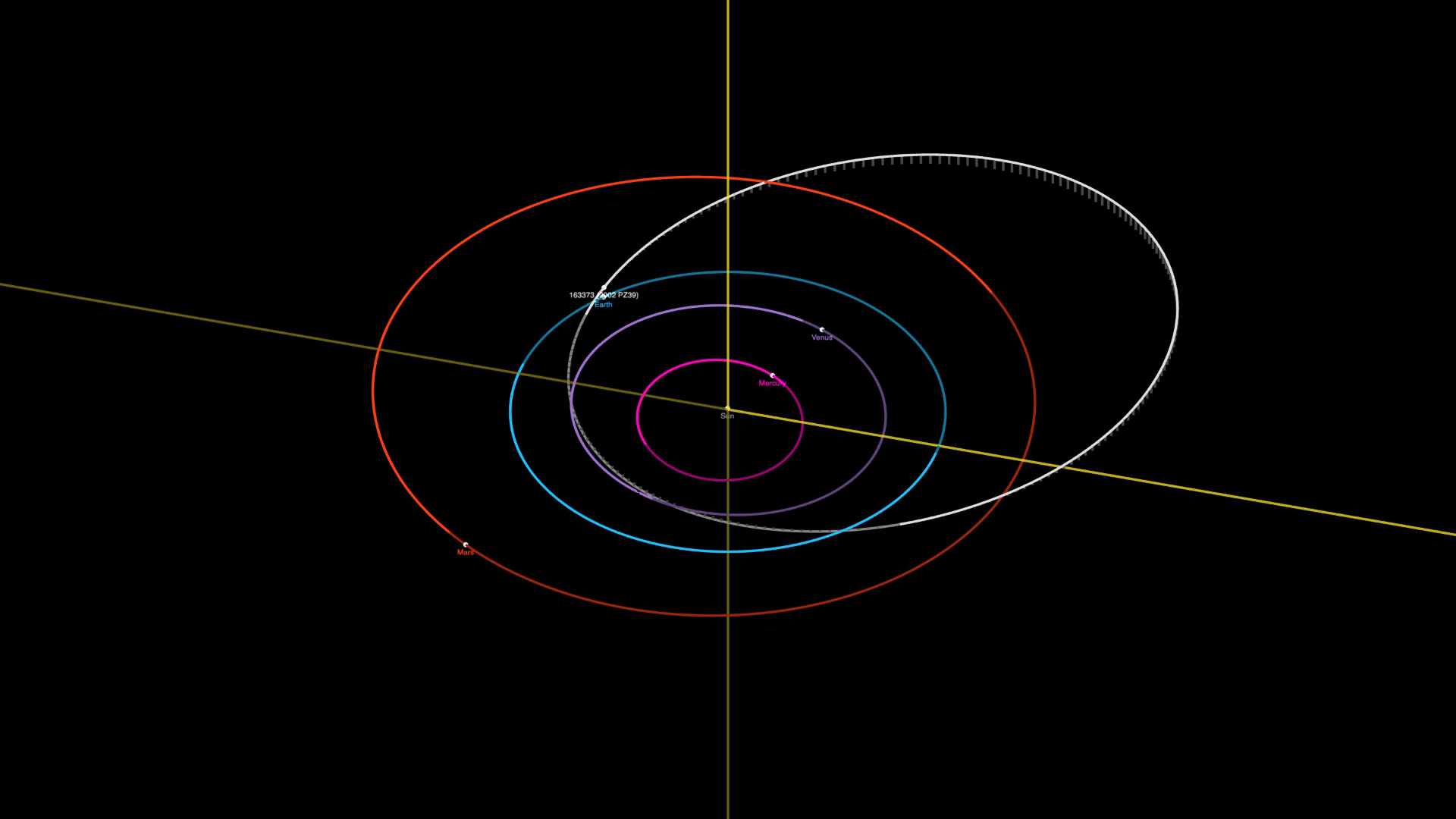
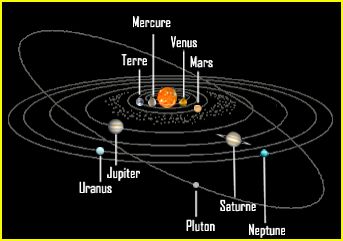
On désigne par variations séculaires des orbites planétaires (VSOP) les changements à long terme présumés (variation séculaire) de l’orbite de toutes les planètes du Système solaire (de Mercure à Neptune). Plusieurs tentatives ont été entreprises pour analyser et prévoir de telles déviations à partir d’orbites ordinaires des satellites. Le problème provient de ce que les planètes ne sont pas seulement sujettes à l'attraction gravitationnelle du Soleil, ce qui conduirait à des orbites elliptiques simples et calculables, mais aussi à divers degrés à celle exercée par leurs propres satellites (lunes) et par les autres objets du Système solaire. Ces forces conduisent à des perturbations de l'orbite qui ne peuvent être calculées de manière explicite. Les orbites peuvent en revanche être approximées par des modèles numériques prenant en compte ces perturbations, souvent au travers de développements en série en fonction du temps.

VSOP est ainsi un modèle moderne numérique utilisable pour l'établissement d'éphémérides des planètes du Système solaire, de Mercure à Neptune.

La théorie semi-analytique VSOP a connu plusieurs moutures depuis son introduction par Pierre Bretagnon (1942 - 2002), en 1982.

• VSOP82: calcul des éléments orbitaux à un instant donné,
• VSOP87: calcul direct de la position (en coordonnées héliocentriques) et des éléments orbitaux,
• VSOP2000: amélioration de la précision d'un facteur 100 à 1000,
• VSOP2002: ajout de corrections diverses (perturbations lunaires, relativité), amélioration de la précision d'un facteur 10,
• VSOP2002b, 2004: prise en compte des perturbations produites par la ceinture d'astéroïdes, par l'aplatissement du Soleil, et par Pluton.

Le cosmos à expansion d'échelle, SEC (ou EST) de C. Johan Masreliez, est un modèle quantitatif théorique, qui décrit de petites variations séculaires d'origine cosmologique. Une telle variation séculaire, provoquée par une traînée de mouvement, est examinée en détail par l'astronome russe Kolesnik avec l'aide théorique de Masreliez (2004). Le résultat est qu'une planète accélèrera en vitesse orbitale, tandis qu'elle tombe lentement vers le Soleil. La relation de variation de la vitesse angulaire est selon la EST,

${\displaystyle {\frac {\mathrm {d} \omega }{\mathrm {d} t}}=3\omega {H_{0}}}$

où ${\displaystyle 1/{H_{0}}}$ est le temps de Hubble et ${\displaystyle \omega }$ est la vitesse angulaire. Ce résultat devrait aider le JPL à corriger ses éphémérides.

Ce petit changement rapproche la Terre du Soleil d'environ 23 mètres par an.

Notes et références

Voir aussi

Articles connexes

• Éphéméride
• Effet Shapiro
• Paramètre post-képlérien
• Cycles de Milankovitch

Liens externes

• La VSOP87 sur l'FTP-Server del Institut de mécanique céleste et de calcul des éphémérides (IMCCE) (Stand: 5. April 2005)
• Masreliez, C.J.; The Expanding Spacetime Theory, (publication populaire), Expanding Spacetime Foundation (2000). (ISBN 0-9665844-1-4). Chapter 5: Evidence of Scale Expanding Spacetime Close to Home.

• Portail de l’astronomie